CBSE Class 12 Math Syllabus 2024.CBSE Class 12 Mathematics Revised Syllabus for the academic session is provided here for students to download in PDF. Students must go through this rationalised syllabus to know the course content prescribed for the current session and understand the examination scheme. CBSE Class 12 Maths Syllabus is in accordance with annual scheme of assessment which mentions the course structure to prepare students for the annual board examination.CBSE Class 12 Math Syllabus .
Unit-I: Relations and Functions
1. Relations and Functions (15 Periods)
Types of relations: reflexive, symmetric, transitive and equivalence relations. One to one and onto functions.
2. Inverse Trigonometric Functions (15 Periods)
Definition, range, domain, principal value branch. Graphs of inverse trigonometric functions.
Unit-II: Algebra
1. Matrices (25 Periods)
Concept, notation, order, equality, types of matrices, zero and identity matrix, transpose of a matrix, symmetric and skew symmetric matrices. Operation on matrices: Addition and multiplication and multiplication with a scalar. Simple properties of addition, multiplication and scalar multiplication. of multiplication of matrices and existence of non-zero matrices whose product is the zero matrix (restrict to square matrices of order 2). Invertible matrices and proof of the uniqueness of inverse, if it exists; (Here all matrices will have real entries).
2. Determinants 25 Periods
Determinant of a square matrix (up to 3 x 3 matrices), minors, co-factors and applications of determinants in finding the area of a triangle. Adjoint and inverse of a square matrix. Consistency, inconsistency and number of solutions of system of linear equations by examples, solving system of linear equations in two or three variables (having unique solution) using inverse of a matrix.
Unit-III: Calculus
1. Continuity and Differentiability (20 Periods)
Continuity and differentiability, chain rule, derivative of inverse trigonometric functions, ???? sin−1 ? , cos−1 ? and tan−1 ?, derivative of implicit functions. Concept of exponential and logarithmic functions. Derivatives of logarithmic and exponential functions. Logarithmic differentiation, derivative of functions expressed in parametric forms. Second order derivatives.
2. Applications of Derivatives (10 Periods)
Applications of derivatives: rate of change of bodies, increasing/decreasing functions, maxima and minima (first derivative test motivated geometrically and second derivative test given as a provable tool). Simple problems (that illustrate basic principles and understanding of the subject as well as reallife situations).
CBSE Class 12 Maths Syllabus Overview
| Unit No. | Unit Name | No. of Periods | Marks |
| I | Relations and Functions | 30 | 08 |
| II | Algebra | 50 | 10 |
| III | Calculus | 80 | 35 |
| IV | Vector and Three-Dimensional Geometry | 30 | 14 |
| V | Linear Programming | 20 | 05 |
| VI | Probability | 30 | 08 |
| Internal Assessment | 20 | ||
| Total | 100 |
Unit I: Relations and Functions
3. Integrals (20 Periods)
Integration as inverse process of differentiation. Integration of a variety of functions by substitution, by partial fractions and by parts, Evaluation of simple integrals of the following types and problems based on them.
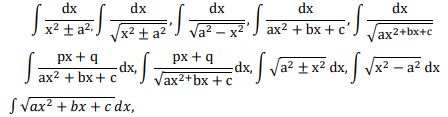
Fundamental Theorem of Calculus (without proof). Basic properties of definite integrals and evaluation of definite integrals.
4. Applications of the Integrals (15 Periods)
Applications in finding the area under simple curves, especially lines, circles/ parabolas/ellipses (in standard form only)
CBSE Class 12 Mathematics Question Paper Design
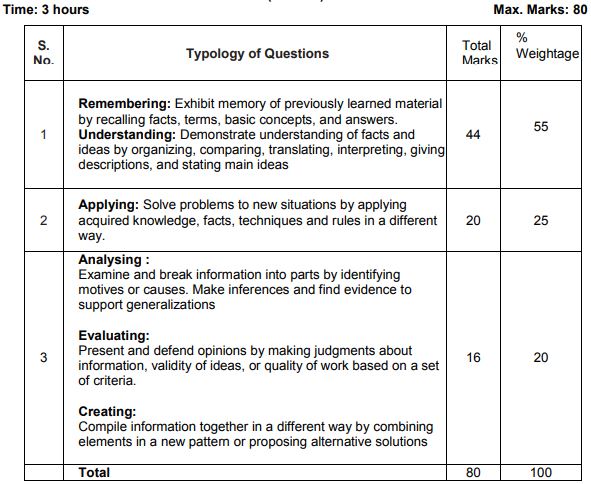
| Typology of Questions | Total Marks | % Weightage |
| Remembering: Exhibit memory of previously learned material by recalling facts, terms, basic concepts, and answers. Understanding: Demonstrate understanding of facts and ideas by organizing, comparing, translating, interpreting, giving descriptions, and stating main ideas. | 44 | 55 |
| Applying: Solve problems to new situations by applying acquired knowledge, facts, techniques, and rules in a different way. | 20 | 25 |
| Analyzing: Examine and break information into parts by identifying motives or causes. Make inferences and find evidence to support generalizations Evaluating: Present and defend opinions by making judgments about information, the validity of ideas, or the quality of work based on a set of criteria. Creating: Compile information together in a different way by combining elements in a new pattern or proposing alternative solutions | 16 | 20 |
| Total | 80 | 100 |
5. Differential Equations (15 Periods)
Definition, order and degree, general and particular solutions of a differential equation. Solution of differential equations by method of separation of variables, solutions of homogeneous differential equations of first order and first degree. Solutions of linear differential equation of the type:

Unit-IV: Vectors and Three-Dimensional Geometry
1. Vectors (15 Periods)
Vectors and scalars, magnitude and direction of a vector. Direction cosines and direction ratios of a vector. Types of vectors (equal, unit, zero, parallel and collinear vectors), position vector of a point, negative of a vector, components of a vector, addition of vectors, multiplication of a vector by a scalar, position vector of a point dividing a line segment in a given ratio. Definition, Geometrical Interpretation, properties and application of scalar (dot) product of vectors, vector (cross) product of vectors.
2. Three – dimensional Geometry (15 Periods)
Direction cosines and direction ratios of a line joining two points. Cartesian equation and vector equation of a line, skew lines, shortest distance between two lines. Angle between two lines.
Unit-V: Linear Programming
1. Linear Programming (20 Periods)
Introduction, related terminology such as constraints, objective function, optimization, graphical method of solution for problems in two variables, feasible and infeasible regions (bounded or unbounded), feasible and infeasible solutions, optimal feasible solutions (up to three non-trivial constraints).
Unit-VI: Probability
1. Probability 30 (Periods)
Conditional probability, multiplication theorem on probability, independent events, total probability, Bayes’ theorem, Random variable and its probability distribution, mean of random variable.
CBSE Class 12 Mathematics Question Paper Design (Code No. 041) :
1. No chapter wise weightage. Care to be taken to cover all the chapters
2. Suitable internal variations may be made for generating various templates keeping the overall weightage to different form of questions and typology of questions same.
Choice(s): There will be no overall choice in the question paper. However, 33% internal choices will be given in all the sections.
Note: For activities NCERT Lab Manual may be referred.
CBSE Class 12th Syllabus All Subjects
| CBSE 12th Class Syllabus | CBSE 12th Class Split up Syllabus |
|---|---|
| English Core | Download View |
| Fine Arts | Download View |
| Hindi | Download View |
| Biology | Download View |
| Chemistry | Download View |
| Physics | Download View |
| math | Download View |
| Political Science | Download View |
| Psychology | Download View |
| Computer Science | Download View |
| Sociology | Download View |
| Physical Education | Download View |
